Pegelrechnung

Pegelrechnung

Allgemeines

In der Kommunikationstechnik spielen die Größen Spannung und Leistung eine große Rolle. Der Spannungswert wird mit der Einheit Volt [V] und der Leistungswert mit der Einheit Watt [W] angegeben, wobei bei Spannungen zur Angabe der Polarität das Minuszeichen verwendet wird.

In der Kommunikationstechnik bestehen Systeme meist aus Kettenschaltungen einzelner Funktionseinheiten. Um die Wirkung solcher Systeme zu veranschaulichen, ist die Angabe des Verhältnisses von Ausgang zu Eingang von großer Bedeutung.

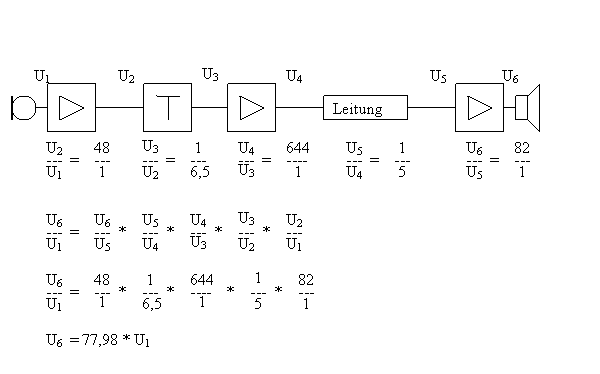
Um sich diese aufwendige Multiplikation zu ersparen, verwendet man den Logarithmus wodurch man die einzelnen Werte einfach addieren kann.

Denn wie man weiß ist lg(a*b*c) = lg(a)+lg(b)+lg(c)

Für die Variablen a, b und c sind nun Verhältnisse einzusetzen (wie zum Beispiel Ausgang zu Eingang).

Verhältnisse werden ja bekanntlich durch einen Bruch beschrieben und sind somit dimensionslos.

Das logarithmierte Verhältnis von Leistungs- und Feldgrößen bezeichnet man als Pegel (engl.: level).

Der Spannungspegel wird mit L_U und der Leistungspegel mit L_P bezeichnet.

Somit erhält man für den Leistungspegel folgende Formel:

L_P=lg(Pa/Pe)    Pa . Ausgangsleistung

Pe . Eingangsleistung

Da die Pegelangaben eigentlich dimensionslos sind, hat man die Pseudoeinheit "Bel" eingeführt. In der Praxis hat sich aber das Dezibel durchgesetzt, weil somit die Zahlenangaben leichter überschaubar sind.

1 B = 10 dB

Daraus folgt für den Leistungspegel:

L_P=10*lg(Pa/Pe) dB

Anhand eines Beispiels wird nun die Formel für den Spannungspegel hergeleitet:

Pe=   42W

Pa= 300W

L_P=10* lg(Pa/Pe)

Wir wissen, dass P=U²/R ist und können somit in obige Gleichung einsetzen:

L_P=10*lg(U²a/Ra)/( U²e/Re)

Als Bedingung gilt, dass sich beide Leistungen auf den gleichen Widerstand beziehen:

Ra = Re

Somit Entfällt der Widerstand aus der Gleichung:

L_U=10*lg(Ua/Ue)²=10*2*lg(Pa/Pe)

Somit ergibt sich für den Spannungspegel:

L_U=20*lg(Ua/Ue) dB

Sind die Ausgangswerte eines Netzes größer als die Eingangswerte so spricht man von Verstärkung (gain), im umgekehrten Fall von Dämpfung (attenuation). Bei Verstärkungen ergibt sich ein positiver Wert für den Pegel und für die Dämpfung ein negativer Wert.

In der Literatur wird aber nicht immer darauf geachtet. So muss man bei der Aussage dass die Dämpfung 12dB beträgt berücksichtigen, dass man in den Berechnungen -12dB für die Dämpfung einsetzt.

Dadurch dass der Pegel ein logarithmisches Maß ist, kann man große Werteverhältnisse überschaubar machen.

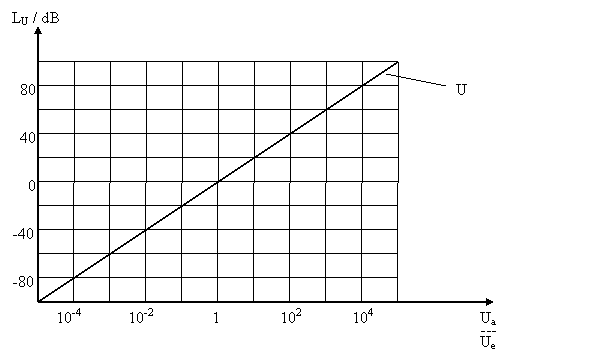
Bisher wurden bei den Spannungs- und Leistungsverhältnissen zwei beliebige Punkte in einem Netz betrachtet. In Netzen ist es aber auch üblich die Leistung bzw. Spannung an einem definierten Punkt als Bezug zu wählen.

Relativer Pegel

Bis jetzt wurden nur Pegel mit beliebigen Referenzwerten behandelt, sie werden als relative Pegel bezeichnet. Der Pegel hängt stets davon ab, welcher Punkt als Bezug gilt.

Absoluter Pegel

Werden bei Pegelangaben definierte Werte als Bezugsgröße verwendet so handelt es sich um absolute Pegel. Um einen solchen absoluten Pegel zu erkennen wird dB durch ein zusätzliches Kürzel ergänzt. Ist die Leistung zum Beispiel auf 1 mW bezogen, so schreibt man dBm.

In der Praxis haben sich folgende Größen mit einem solchen Kürzel durchgesetzt:

dBm           Absoluter Leistungspegel, bezogen auf 1 mW

dBW           Absoluter Leistungspegel, bezogen auf 1 W

dBµV                   Absoluter Spannungspegel, bezogen auf 1 µV

dBV           Absoluter Spannungspegel, bezogen auf 1V

Hier ein kleines Beispiel zur Veranschaulichung der Umrechnung:

U = 0,224V 

20*lg(0,224/1µ)= 107dBµV 

Da durch das Kürzel erkennbar ist dass es sich um einen absoluten Pegel handelt, kommt der Begriff "absolut" in der Literatur so gut wie nie vor.

Pegelplan

Da Kommunikationssysteme aus verschiedenen Funktionseinheiten bestehen, die durch Dämpfung und Verstärkung gekennzeichnet sind, ist es von Vorteil diese Eigenschaften abhängig vom Ort in einem Diagramm darzustellen. Der so genannte "Pegelplan" ist die Darstellung des Pegels in Abhängigkeit vom Ort in einem Kommunikationssystem. Auf der x-Achse wird der Ort x aufgetragen und auf der y-Achse der Pegel.

In folgendem Beispiel wird der Pegelplan eines 5 stufigen Kommunikationssystems dargestellt:

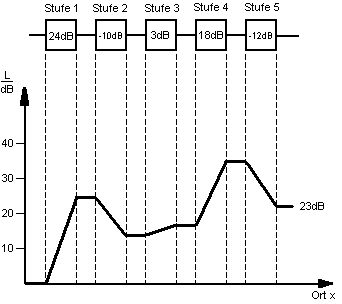
Im Pegelplan können relative Pegel, aber auch absolute Pegel dargestellt werden. Ist am Eingang ein absoluter Pegel vorhanden, dann ergibt sich auch am Ausgang ein absoluter Pegel. Aus dem Diagramm ist beim absoluten Pegel auch ersichtlich welcher größte und kleinste Pegel im Kommunikationssystem auftaucht.