Digitale Signalverarbeitung
Legt man an einem Eingang eines Netzwerkes unterschiedliche Signalformen an, so treten im Netzwerk, je nach Bauteile, unterschiedlichste Signalformen auf.
Beim Anlegen eines sinusförmigen Signales stellt man fest, daß überall im Netzwerk wieder sinusförmige Signale gleicher Frequenz autreten. Sie unterscheiden sich nur in Betrag und Phase.
Da man weiß, daß überall in Netzwerk nur sinusförmige Größen auftreten, kann man für alle Signale einen sinusförmigen Ansatz machen:
![]()
Es zeigt sich, daß Winkelfunktion mathematisch viel schwieriger zu behandeln sind, als komplexe Zeiger. Man setzt daher die Signale als komplexe Zeiger an, das meßbare Signal ist dann der Realteil davon.
![]()
daraus folgt
![]()
Um den Realteil einer Cosinusschwingung darzustellen, können wir mit Hilfe der Euler´schen Formel
![]()
und der daraus abgeleiteten Beziehungen
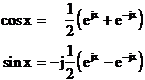
folgenden Ansatz durchführen:
![]()
![]()
oder allgemein
![]()
Diese Formel ist auch recht anschaulich in Abb.1 zu sehen.
![]()
Die physikalische Realität der cosinusförmigen Schwingung, beispielsweise der zeitliche Verlauf einer Spannung, wird also durch ein Modell zweier Zeiger dargestellt, die gegensinnig in der komplexen Ebene mit der Winkelgeschwindigkeit w rotieren. Ihre vektorielle Addition ergibt den Momentanwert der Cosinusschwingung. Dieser Wert ist immer eine reelle Größe trotz der komplexen Anteile der beiden Zeiger (siehe Abb.1). Babei ordnen wir dem in positiver Richtung umlaufenden Zeiger die positive Umlauffrequenz +w, dem gegensinnig rotierenden Zeiger die negative Frequenz -w zu.
Wir müssen uns darüber im klaren sein, daß dem realen physikalischen Vorgang nur eine positive Frequenz w zukommt, daß wir aber eine negative Frequenz -w hinzunehmen müssen, wenn wir unsere Modellvorstellung der rotierenden Zeiger (oder komplexen Zeiger) verwenden, um beispielsweise den Verlauf einer Spannung richtig voraussagen zu können.
Bei der Darstellung des komplexen Zeigers kann neben der schon in Abb.1 gezeigten Veranschaulichung mit dem rotierenden Zeiger auch ein Betrags- und Phasenspektrum verwendet werden. Es ist zu unterscheiden zwischen dem einseitigen Spektrum und den 2-seitigen Spektrum mit der negativen Frequenz (siehe Abb.2).
|
einseitiges Spektrum |
zweiseitiges Spektrum |
|
|
|
|
|
|
Abb.2
Bei der Untersuchung von Netzwerken ergibt sich eine nützliche analytische Erweiterung der gewohnten Beschreibung stationärer Sinusschwingungen durch die Einführung der komplexen Frequenz
![]()
In der gewohnten Zeigerdarstellung erhält man dadurch den komplexen Augenblickswert:
![]() .
.
Durch diese Einführung der komplexen Kreisfrequenz p
erhalten wir nun eine einheitliche Darstellung sowohl für stationäre als auch
für an- bzw. abklingende Sinusschwingungen (siehe Abb.3). Bislang haben wir
nur mit einem Sonderfall der komplexen
Frequenz gerechnet- dem stationären Zustand(![]() ).
).
Abb.3
Wie jede komplexe Zahl, kann auch die komplexen Kreisfrequenz p in der Gaußschen Zahlenebene dargestellt werden. Man spricht dann von der Ebene der komplexen Kreisfrequenz oder p-Ebene (siehe Abb.4).
komplexer Augenblickswert:
![]()
dabei ist
![]() Strecker
Strecker
![]() Dreher
Dreher
Abb.4
Der physikalischer Augenblickswert ist
![]()
Bis jetzt haben wir immer vorweggenommen, daß man einfach mit komplexen Zahlen ein Netzwerk aus Widerständen, Kapazitäten, Induktivitäten darstellen kann.
Allgemein gilt für jede Zeitfunktion:
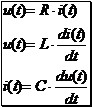
Da uns nur sinusförmige Größen interessieren und alle Ströme und Spannungen im linearen Netzwerk mit sinusförmiger Erregung (Frequenz f) selbst wieder sinusförmig sind (Frequenz f), können wir die Rechnung vereinfachen.
ohmscher Widerstand:
|
|
|
![]()
oder mit den Effektivwerten: ![]()
Bei einem ohmschen Widerstand sind Strom und Spannung in Phase.
Induktivität:
Bei der
Einführung der komplexen Frequenz trat anstelle des "Drehers" ![]() der "Drehstrecker"
der "Drehstrecker" ![]() . Man kann daher in linearen Netzen
Ströme und Spannungen auch durch diese Drehstrecker darstellen(analytische
Erweiterung).
. Man kann daher in linearen Netzen
Ströme und Spannungen auch durch diese Drehstrecker darstellen(analytische
Erweiterung).
Anmerkung: Alle p (komplexe Frequenz) sind komplex und daher zu unterstreichen
|
|
|
oder mit
den Effektivwerten: ![]()
Bei
einer Induktivität eilt die Spannung dem Strom um ![]() vor (bei harmonischer Schwingung)
vor (bei harmonischer Schwingung)
Kapazität:
Die selbe Vorgehensweise kann auch bei der Kapazität vorgenommen werden.
|
|
|
oder mit
den Effektivwerten: ![]()
Bei
einer Kapazität eilt der Strom der Spannung um ![]() vor
vor
Normalerweise müßten wir um Ströme und Spannungen in einem Netzwerk berechnen zu können, eine Differentialgleichung aufstellen und diese dann lösen. Da wir einmal voausgesetzt haben, daß wir uns auf sinusförmigen Größen beschränken, vereinfacht sich die Rechnung von einer Differentialgleichung zu einer algebraischen Gleichung, die eigentlich kein Problem bei der Lösung darstellen sollte.
![]()
![]()
![]()
Berechnung siehe nächste Seite !!
Für sinusförmige Größen:
![]()
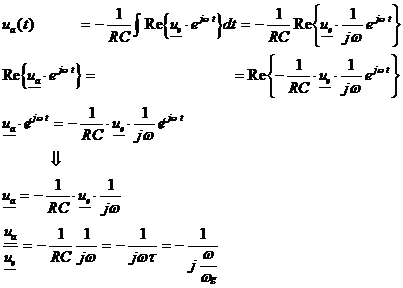
Aufgrund das in einem linearen System bei Anregung mit sinusförmigen Größe an jedem Punkt des Netzwerkes wieder eine sinusförmige Größe gleicher Frequenz auftritt, kann die Ausgangsspannung auch als sinusförmig angenommen werden.
Da definitionsgemäß zwei Realteile nur gleich sind wenn ihre Argumente gleich sind, kann die Realteilbildung entfallen.Schließlich erhält man eine Funktion die nur mehr eine Funktion der Frequenz ist.
Aus der obigen Beziehung erhält man, wenn man eine sinusförmige Spannung an den Eingang legt, eine sinusförmige Spannung gleicher Frequenz, jedoch anderer Amplitude und Phasenlage.
Dieser Punkt soll zur Übersicht der Transformationen zwischen dem Zeitbereich und dem Frequenzbereich dienen
![]() Zeitbereich Frequenzbereich
Zeitbereich Frequenzbereich
![]()
![]()
![]()
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Die letzten zwei Transformationen zeigen, daß man eine wichtige Vereinfachung bei der komplexen Zeigerrechnung vornehmen kann:
![]() Diff.gleichung algebr.Gleichung
Diff.gleichung algebr.Gleichung
Sehr oft begegnen wir in der Elektronik mehr oder weniger komplizierten Zeitfunktionen wie bspw. einer Folge von Rechteckpulsen, die einen periodischen Verlauf aufweisen. Fourier zeigte, daß man periodische Funktionen durch eine Summe von Sinus- und Cosinusfunktionen darstellen kann. Dies führt auf die bekannte Fourierreihe eines periodischen Signales:
![]()
Der Gleichanteil ist definiert als
![]()
Wie man sich durch Nachrechnen
überzeugen kann, erhält man die Amplituden An und Bn,
wenn man die obige Gleichung mit ![]() oder
oder ![]() multipliziert und über
eine Periode des Signals, bspw. über [0,T] integriert.
multipliziert und über
eine Periode des Signals, bspw. über [0,T] integriert.
![]() und
und ![]()
Man kann die Summe von Cosinus- und Sinusschwingungen durch eine Summe von Cosinus- bzw. Sinusschwingungen bestimmter Phasenlage wie folgt ersetzen
![]()
bzw.
![]()
mit folgenden Zusammenhänge (siehe Abb.5)
![]()
und
![]() bzw.
bzw. ![]()
Ist f(t) eine gerade Funktion,
also f(-t) = f(t), so treten in der Gleichung ![]() wegen Bn =
0 nur Cosinusglieder auf. Ist das Signal f(t) dagegen ungerade, also
s(-t)=-s(t), so besteht die Gleichung nur aus Sinusgliedern, da An = 0.
Bei allen übrigen Funktionen treten Sinus- und Cosinusglieder gemeinsam auf.
wegen Bn =
0 nur Cosinusglieder auf. Ist das Signal f(t) dagegen ungerade, also
s(-t)=-s(t), so besteht die Gleichung nur aus Sinusgliedern, da An = 0.
Bei allen übrigen Funktionen treten Sinus- und Cosinusglieder gemeinsam auf.
Abb.5
Mit Hilfe der Gleichungen
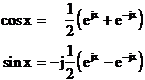
wird aus der reellen Fourierreihe die komplexe Fourierreihe,
![]()
wobei sich die komplexen Amplituden Cn, auch als Fourierkoeffizienten bezeichnet, wie folgt berechnen lassen:
![]()
Diese Formel läßt sich folgendermaßen anschaulich erklären:
Allgemein gilt nämlich:
![]()
stellt man sich nun die Funktion wie folgt vor:
![]()
und multipliziert sie mit ![]() , so wird das Produkt mit Cn gleich 1 und
der Fourierkoeffizient bleibt über, da die anderen Summanden 0 ergeben.
, so wird das Produkt mit Cn gleich 1 und
der Fourierkoeffizient bleibt über, da die anderen Summanden 0 ergeben.
Wie aus Abb.5 ersichtlich ist, ist
![]()
bzw. der konjugiert komplexe Zeiger
![]()
Wie schon vorher erwähnt ist
![]()
Die Formel kann nun auch mit dem konjugiert komplexen Zeiger angeschrieben werden:
![]()
Es besteht auch folgender Zusammenhang, der auch in der Abbildung 5 ersichtlich ist:
![]()
und
![]()
wenn n=0, läßt sich folgende Vereinfachung durchführen
![]()
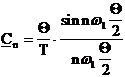
Abb.6
Bei der Entwicklung eines periodischen Signal in eine Fouriereihe erhalten wir eine Summe von harmonischen Schwingungen mit einem Frequenzabstand von Dw
Ein nicht periodisches Signal kann man als periodisches Signal mit der Periode T auffassen.
Wir gehen zuerst vom Spektrum der komplexen Fourierreihe aus:
|
|
Abb.7 |
In diese Formel setzen wir das Integral zur Berechnung von Cn ein. Mit w1 = Dw erhalten wir dann:
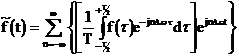
Diese Formel wird nun mit ![]() erweitert:
erweitert:
|
|
Abb.8 |
Anschaulich ist das eine Summe von Rechtecken.
Macht man diese Rechtecke nun immer schmäler (im Zeitbereich bedeutet das, daß die Periode des Zeitsignales immer größer wird), wird aus der Summe der Rechteckflächen die Fläche unter der Funktion F(w).
|
|
Abb.9 |
Aus der Fourierreihe wurde das Fourierintegral.
Im folgenden Kasten sind die beiden wichtigen Fourierintegrale noch einmal zusammengefaßt.
Die erste Gleichung wird als Fouriertransformation bezeichnet - die Zeitfunktion f(t) wird in den Frequenzbereich "transformiert", wo ihr die Amplitudendichte F(w) entspricht. Die zweite Gleichung wird als Fourier-Rücktransformation bezeichnet.
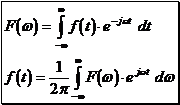
In der Nachrichtentechnik werden meist die zwei Formel in der allgemeinen Form angeschrieben:
mit
![]()
wird dann
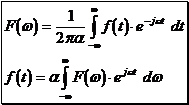
Wie man in Abb.8 und der Formel
gut erkennen kann, besitzt das einzelne Rechteck die Höhe ![]() . Multipliziert man diesen Wert mit Dw, so erhält man die Fläche
des Rechteckes.
. Multipliziert man diesen Wert mit Dw, so erhält man die Fläche
des Rechteckes.
Durch diese Herleitung kann man schön den Zusammenhang zwischen F(nDw) und Cn erkennen. Schlußendlich kann folgende Beziehung aufgestellt werden:
![]()
Durch diesen Zusammenhang kann man, wenn das Spektrum eines (Einzel)Impulses bekannt ist, sofort die Fourierreihe eines Pulses, sprich eine periodische Impulsfolge, erhalten !!
Definition:
|
|
für |t| 0,5(-t1): rect(t)=1
für |t|>0,5(+t1): rect(t)=0
Abb.10
Berechnung des Frequenzspektrums dieses Rechtecks:
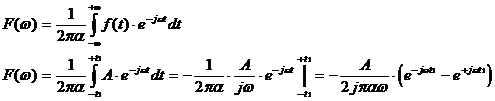
mit
![]()
erhält man:
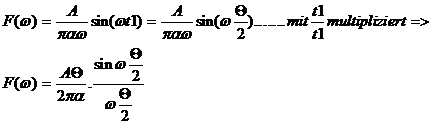
Als Ergebnis erhält man also eine sogenannte-
SI-Funktion:
Nullstellenberechnung:0-Stellen sind vorhanden wenn gilt:
wt1 = np
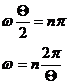
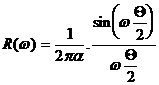
Abb.11
Macht man den Rechteckimpuls schmäler, so wirkt sich diese Verschmälerung so auf die Übertragungsfunktion des System aus, daß die Nullstellen immer weiter nach außen wandern.
Beim Dirac-Impuls erhält man dann schließlich ein konstantes Spektrum.
Um von einem Rechteckimpuls zu einem Diracimpuls zu gelangen, muß man die Impulsdauer Q bis Null verkleinern.
Berechnung der Systemantwort über den Frequenzbereich:
Mit Hilfe des Dirac-Impulses läßt sich die Übertragungsfunktion eines Systemes ermitteln:
allgemein gilt nämlich:
h(t). Impulsantwort
Zunächst wird die Impulsantwort eines Tiefpasses untersucht:
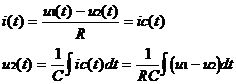
Für sehr "schmale" Impulse gilt folgendes:
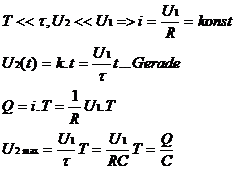
Je kürzer die Dauer des Eingangspulses r(t) bei konstantgehaltener Fläche wird, umso mehr nähert sich das Ausgangssignal einer Form, die nur noch von den Eigenschaften des Übertragungssystemes und nicht mehr von der Dauer des Eingangsimpulses abhängt, an.
Die Berechnung der Systemantwort im Zeitbereich:
Darstellung des Eingangssignal als eine Summe von Rechteck- / Diracimpulsen:
|
Rechteckimpuls: |
|
Aufgrund dieser Erkenntnisse, kann man jetzt, von so(t) ausgehend, die Reaktion g(t) des Systems, auf ein beliebiges Eingangssignal s(t) näherungsweise bestimmen. Dabei nähert man das gegebene Eingangssignal mit lauter amplitudenbewerteten Rechteckimpulsen an, sodaß man eine Treppenfunktion fT(t) erhält.
Es gilt nun für fT(t):
![]()
![]()
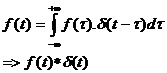
d(t-t) sind Dirac-Impulse, die mit f(t) bewertet werden und um t zeitverschoben sind.
Es gilt nun für gT(t):
![]()
![]()
![]() allgemeines Faltugsintegral
allgemeines Faltugsintegral
r(t) .. Antwort auf einen Rechteckimpuls
h(t) Antwort auf einen Diracimpuls
g(t) Antwort auf eine beliebige Funktion f(t)
Diese Faltungsintegrale, die wie man sieht eine Verknüpfung zwischen der Reaktion g(t), eines Systems, seiner Stoßantwort h(t) und dem Eingangssignal f(t) herstellt, kann man auch abkürzend als sogenanntes Faltungsprodukt anschreiben:
|
|
g(t)=f(t)*h(t
Das Operationszeichen in der Gleichung heißt Faltungsstern. Die Operation der Faltung ist nach den selben Rechenregeln wie die Multiplikation zu verwenden.
Es gilt das:
Kommutativgesetz:
g(t) = s(t) * h(t) = h(t) * s(t)
Assoziativgesetz:
f(t) * s(t) * h(t) = [f(t) * s(t)] * h(t) = f(t) * [s(t) * h(t)]
Distributivgesetz:
f(t) * [s(t) + h(t)] = [f(t) * s(t)] + [f(t) * h(t)]
Um die Gewichtsfunktion g(t) eines Eingangssignales f(t) zu erhalten, muß man für eine Anzahl von Zeitpunkten t das Integral (Fläche unter der Kurve) bestimmen.
Dazu formt man das Faltungsintegral um:
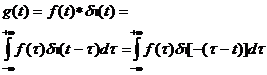
Faltung mit d(t-T) bedeutet eine Verschiebung der Funktion um T.
Haupt | Fügen Sie Referat | Kontakt | Impressum | Nutzungsbedingungen
