Regelkreis

Um die Funktionsweise des PLL besser zu verstehen muß zuerst der Überbegriff des Regelkreises näher erörtert werden. Grundsätzlich muß man zwischen Steuerung und Regelung unterscheiden:

Bei der Steuerung ist der Ausgangsgröße nur eine Eingangsgröße zugeordnet. Ist das System vollständig bekannt und treten keine unkontrollierbaren Störungen auf, so kann der zeitliche Verlauf der Eingangsgröße so vorgegeben werden, daß das gewünschte Ausgangssignal auftritt.

Da aber meist Störungen auftreten, die im Einzelnen nicht bekannt sind und deren Verläufe nicht vorhersehbar sind, ist es erforderlich, die Ausgangsgröße zu beobachten. Aus dieser so gewonnenen Information, kann nun die Eingangsgröße in geeigneter Weise verändert werden. Man spricht dann von einer Regelung, oder einem Regelkreis.

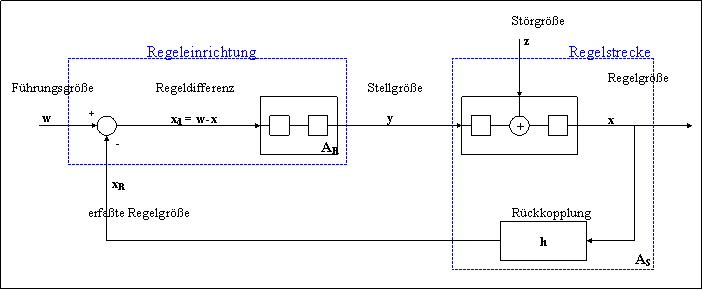
Meist soll eine zeitlich veränderliche Größe beeinflußt werden. Die zu beeinflussende Größe wird als Regelgröße x bezeichnet, das System als Regelstrecke oder kurz Strecke. Die Ausgangsgröße der Strecke ist die Regelgröße. Durch Störungen, die auf die Regelstrecke eingreifen, wird die Regelgröße beeinflußt. Die Störgröße wird mit z bezeichnet. Im Rückkopplungszweig h wird die Regelgröße erfaßt, um sie auf den gewünschten zeitlichen Verlauf zu bringen. Oft wird die Regelgröße in eine andere physikalische Größe umgewandelt, um sie besser verarbeiten zu können. Die so erfaßte Regelgröße x_R ist der Regelgröße im stationären Zustand proportional. x_R wird nun mit der Führungsgröße w, oder auch Sollwert, durch Differenzbildung verglichen, die Regeldifferenz x_d, ist demnach w-x_R. Ist die Regeldifferenz gleich null, so ist die Regelgröße x gleich dem Sollwertverlauf. Ist x_d aber von null verschieden, so wirkt diese auf die Regelstrecke ein. Dabei wird versucht die Regelgröße x dem Sollwertverlauf wieder anzugleichen.

Ein Beispiel für die Notwendigkeit der Regelgröße in eine andere physikalisch Größe bietet die Temperaturregelung: Es soll mittels einer Regelung die Temperatur eines Raumes auf konstantem Wert (z.B.20°C) gehalten werden. Die Regelgröße ist nun eine Temperatur. Um die Eingangsgröße verändern zu können, ist es notwendig die Temperatur in eine elektrische Größe umzuwandeln, um regeln zu können.

A_R .. Verstärkung des Reglers

A_S .. Verstärkung der Strecke

Für lineare Systeme gilt:        y = A_R(w-x) x = A_S(y+z)

Damit ergibt sich für x:         

Führungsverhalten:               

Störverhalten:                        

Das Führungsverhalten ist um so besser, je größer die Schleifenverstärkung A_RA_S ist. Im Idealfall  wäre das Führungsverhalten gleich 1. Das Störverhalten hingegen wird um so besser (im Idealfall 0), je größer die Verstärkung des Reglers A_R wird. Jedoch darf man die Schleifenverstärkung nicht beliebig groß machen, da sonst die Phasenverschiebungen im Regelkreis, die unvermeidbar sind, zu Schwingungen führen und daraus folgend zur Instabilität. Die Aufgabe eines Regelkreises besteht nun darin, trotz dieser Einschränkung, eine möglichst kleine Regeldifferenz und gutes Einschwingverhalten zu erzielen.

Als besondere Anwendung eines Regelkreises kann nun die PLL näher behandelt werden.