Fuzzy-Regler
Fuzzy bedeutet unscharf. Die Fuzzy Logic ermöglicht die Interpretation von Aussagen die nicht eindeutig als wahr oder falsch eingestuft werden können.
Beispielsweise können Variablen durch Begriffe wie "relativ groß" oder "zu schnell" beschrieben werden, was bei normalen mathematischen Anwendungen nicht möglich ist. Dies bedeutet auch, daß eine Zahl, die in einen bestimmten Wertebereich fällt, diesem nicht ganz einfach angehört, sondern es existiert ein gewissen Grad an Zugehörigkeit, d. h. die Zahl kann mehr oder weniger wahr sein. Es gibt daher nicht nur richtig oder falsch, sondern auch zahlreiche dazwischen liegende Abstufungen, und vor allem Schlußfolgerungen nach dem 'Je mehr , desto ' Prinzip.
Fuzzy -Regler haben gegenüber herkömmlichen Reglern einige Vorteile:
Nichtlineare Vorgänge können wesentlich einfacher beschrieben werden
Fuzzy -Controller erzeigen meist ein stabileres und robusteres Verhalten
Das Wissen aus Testreihen kann in der Entscheidungstabelle verwertet werden
Man benötigt kein genaues mathematisches Modell
Durch die Form der Regeln ist das Verhalten des Reglers auch für Laien verständlich
Übersicht:
unscharfer
Bereich

![]() Regelblatt
Regelblatt

Fuzzyfizierung Defuzzyfizierung

SYSTEM
deterministischer
Bereich
Fuzzyfizierung:
Die Eingangswerte sind als linguistische Variablen aufzufassen, deren Wertebereich und physikalische Größen festzulegen sind. Danach muss die Ausprägung der Variablen und ihre Zuordnung zu Fuzzy-Sets bestimmte werden. Es müssen Zugehörigkeitsfunktionen für die einzelnen Fuzzy-Sets gefunden werden.
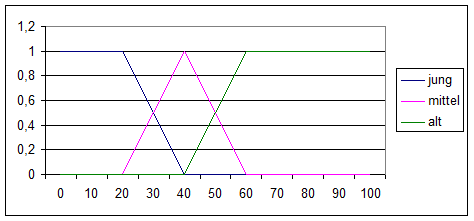
Bsp: Fuzzy Set:
Die Verteilungskurven können jede mathematisch beschreibbare Funktion annehmen.
z.B.: 45Jahre = 0% Jung
75% Mittel
25% Alt
Um verschiedene unscharfe Mengen miteinander zu verknüpfen benötigt man Operatoren:
UND -Verknüpfung:
mC = MIN (mA mB
Mittel und Alt MIN (0,75;0,25) = 0,25
ODER -Verknüpfung
mE = MAX (mA mB
Mittel oder Alt MAX (0,75;0,25) = 0,75
NICHT - Operation
mN mA
NICHT alt
BSP: Temperaturregelung:
Mit Hilfe der Messgrößen DT und T soll eine Heizung auf den gewünschten Sollwert geregelt werden.
Messgößen: Temperaturabweichung T
Temperaturänderung DT
Stellgröße: Heizung
Temperatutabweichung:
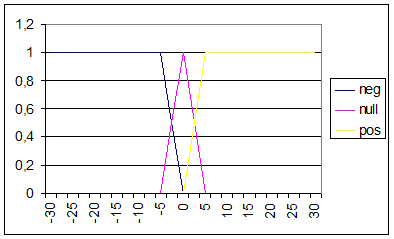
Temperaturtendenz:
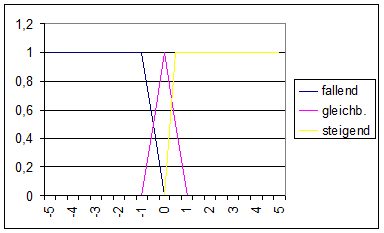
Heizung:
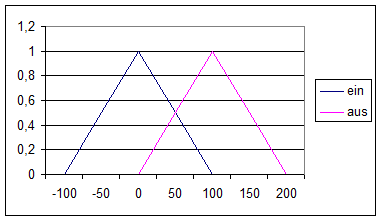
Entscheidungstabelle:
Anhand der Fuzzy Sets muss nun bestimmt werden für welche Eingangswerte welcher Ausgangswert in Frage kommt.
|
dTT |
neg |
null |
pos |
|
fallend |
ein |
ein |
aus |
|
gleichbl. |
ein |
aus |
aus |
|
steugend |
ein |
aus |
aus |
Regelbank:
Die Entscheidungstabelle wird nun in Regelform dargestellt. Diese sind in der einfachen WENN- DANN -Form dargestellt, sind dadurch sehr flexibel, was die Erweiterbarkeit, die Modifizierbarkeit, und die Verständlichkeit anbelangt.
WENN T = neg DANN Heizung ein
WENN T = pos DANN Heizung aus
WENN (T = null UND DT = fallend) DANN Heizung ein
WENN (T = null und DT nicht fallend) DANN Heizung aus
Die Ergebnisse für Heizung ein und Heizung aus werden jeweils miteinander ODER-Verknüpft. Wenn also mehrere Werte für ein Ausgangsdreieck vorhanden sind, gilt nur der größte.
Zur Überprüfung der Regelbank können verschiedene Teperaturwerte angenommen werden und in die Regeln eingesetzt werden.
Defuzzyfizierung:
Da die so errechneten Werte unscharf sind, muss man sie mit Hilfe verschiedener Methoden wieder auf einen scharfen wert zurückrechnen.
1)Max/Min und Max/Prod -Methode:
Bei beiden Methoden wird rechnerisch der Flächenschwerpunkt der Dreiecke ermittelt
Der Unterschied zwischen den Beiden Methoden liegt in der aufteilung der Fläche unter den Dreiecken
Bei der MAX/MIN - Methode wird die Fläche unter dem Dreieck, die über dem ermittelten Wert der Zugehörigkeit liegt nicht mit eingerechnet.
Bei der MAX/PROD -Methode wird die Fläche unter neuen Dreiecken ermittelt, deren Breite Ident mit den ursprünglichen Dreiecken ist, deren Höhe allerdings abhängig von der Zugehörigkeit variiert.
Beide Lösungsmethoden verwenden folgende Formel zur Defuzzyfizierung:
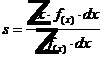
Haupt | Fügen Sie Referat | Kontakt | Impressum | Nutzungsbedingungen
