Wegintegrale und Kurvenintegrale

Wegintegrale und Kurvenintegrale

Theorem 1:

Sei F ein auf dem C¹ Weg stetiges Vektorfeld und sei eine Reparameterisation von s

Wenn r richtungs-wahrend ist, dann gilt

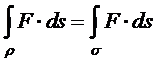
und wenn r richtungs-wechselnd ist, dann gilt

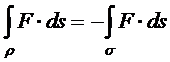
Beispiel:

Sei und sei definiert durch . Rechnen Sie und aus.

Lösung:

Für s haben wir und . Daraus folgt

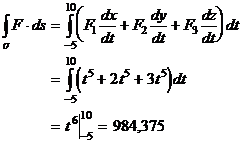
Für

haben wir

und . Daraus folgt

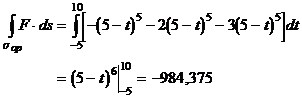
Theorem 2:

Sei s stückweise C¹, f eine stetige (reellwertige) Funktion auf dem Bild von s und sei r irgendeine Parametrisierung von s. Dann gilt:

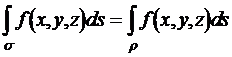
Das nächste Theorem liefert eine nützliche Technik für das Ausrechnen von Kurvenintegralen: Es stellt eine Verallgemeinerung des Fundamentalsatzes 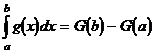dar.

Theorem 3:

Angenommen ist aus der Klasse C¹ und daß ein stückweise C¹ Weg ist. Dann gilt:

(Beachte: für reellwertige Funktionen!)

Beweis:

Wendet man die Kettenregel auf die zusammengesetzte Funktion

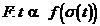
an, so erhält man

Die Funktion F ist eine reellwertige Funktion mit der Variablen t. So folgt also nach dem Fundamental-satz

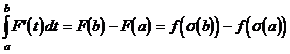
Daraus folgt:

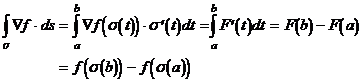
Beispiel:

Sei s der Weg 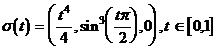. Berechnen Sie

Lösung:

Wir erkennen, daß ydx + xdy bzw. das Vektorfeld yi + xj + 0k genau der Gradient der Funktion ist. So folgt

Definition:

Wir definieren eine einfache Kurve C als das Bild einer stückweise C¹ Abbildung , die auf dem Intervall I bijektiv ist. s wird eine Parametrisierung von C genannt. Eine einfache Kurve ist also eine Kurve, die sich selbst nicht schneidet.

Wenn I = [a,b], dann nennen wir s(a) und s(b) die Endpunkte der Kurve. Jede einfach Kurve hat zwei Orientierung oder Richtungen, die mit ihr verbunden sind. Wenn P und Q die Endpunkte der Kurve sind, dann kann die Kurve C entweder von P nach Q oder von Q nach P gerichtet sein. Die einfache Kurve zusammen mit ihrer Richtung nennt man orientierte einfache Kurve oder gerichtete einfache Kurve.

Definition:

Unter einer einfachen geschlossenen Kurve versteht man das Bild einer stückweise C¹ Abbildung , die auf [a,b) bijektiv ist und die Eigenschaft s(a) = s(b) erfüllt. Erfüllt s die Bedingung s(a) = s(b), ist aber nicht notwendiger Weise bijektiv auf [a,b), so nennt man sie geschlossene Kurve.

Einfache geschlossene Kurven besitzten zwei Orientierungen, also die zwei möglichen Richtungen, sich entlang der Kurve zu bewegen.

Beispiel:

Sei und , mit

Dann ist

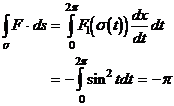
Aber

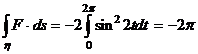
Es ist klar, daß s und h dasselbe Bild haben, nämlich den Einheitskreis in der xy-Ebene, und daß sie den Einheitskreis in derselben Richtung beschreiben. Trotzdem ist . Der Grund hierfür ist, daß s eine bijektive Abbildung ist, h aber nicht (h beschreibt den Einheitskreis zweimal). Daher ist h keine Parametrisierung des Einheitskreises als eine einfache geschlossene Kurve.

Beispiel:

Die Kurve C (gegen den Uhrzeigersinn orientiert) beschreibt uns das Einheitsquadrat in . Berechnen Sie das Kurvenintegral

Lösung:

(1) Wir berechnen das Integral mit Hilfe einer Parametrisierung von C, welche die gegebene Orientierung hervorruft.

z.B.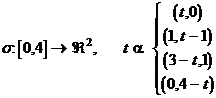

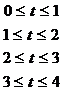
Dann ist

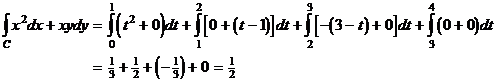
(2) Nun werden wir das Integral noch einmal berechnen, nur daß wir dabei die Kurve zuerst in vier Teilkurven C_i zerlegen und danach alle einzeln parametrisieren.

Zu beachten: , wobei C_i die orientierten Kurven in der Zeichnung sind. Diese werden nun wie folgt parametrisiert:

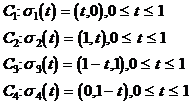
So folgt:

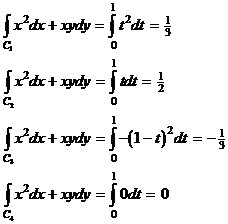
So bekommen wir wieder: