1. Einleitung: Was ist eigentlich "lineare Optimierung"?

Die lineare Optimierung ist ein Teilgebiet der Optimierungsrechnung. Diese Rechnung ist ein Hilfsmittel zur optimalen Entscheidungsfindung bei komplizierten Problemen.

Unter einschränkenden Bedingungen wird mit Hilfe der linearen Optimierung das Minimum beziehungsweise das Maximum einer linearen Funktion ermittelt. Die zu maximierende Funktion ist dabei meistens die Gleichung für den Gewinn, die zu minimierende Funktion die Gleichung für die Kosten eines Unternehmens.

Die einschränkenden Bedingungen, die Einfluss auf das Ergebnis haben, müssen herausgefunden werden, um sie dann mit dem zu erreichenden Maximum / Minimum in Verbindung zu setzen.

2. Geschichte der "linearen Optimierung"

Die lineare Optimierung gehört zu den jüngeren Anwendungsgebieten der Mathematik. Vor einem halben Jahrhundert begann der richtige Durchbruch der linearen Optimierung mit der Simplexmethode, die von G.B. Dantzig entwickelt wurde. Die ersten Arbeiten der Linearen Optimierung wurden im Jahre 1939 von dem russischen Mathematiker Leonid W. Kantorowicz in diesem Gebiet veröffentlicht.

Besonders in den USA wurden am Ende des zweiten Weltkrieges neue Lösungsmöglichkeiten für Probleme der mathematischen Optimierung, die für den militärischen Bereich von Bedeutung waren, entwickelt.

Die Simplexmethode, mit der alle linearen Optimierungsprobleme gelöst werden können, ist bis heute das wichtigste Verfahren zur Lösung von Problemen dieser Art.

J. von Neumann und O. Morgenstern gelang es schon kurz nach Dantzig diese Methode beträchtlich weiterzuentwickeln. Seit Beginn der 50er Jahre erlebte dieser Bereich der Mathematik erneut eine rapide Aufwärtsentwicklung. Dieser große Aufschwung wirkte sich besonders günstig auf Großrechenanlagen aus, die Berechnungen nach dem Simplexverfahren in einer kurzen Zeit bewältigen konnten. Schon im Jahre 1956 konnten mit einer IBM- Maschine Probleme der linearen Optimierung mit mehr als 200 Gleichungen mit großer Genauigkeit gelöst werden. Die erste wichtige Anwendung auf wirtschaftliche Probleme erfolgte bei der Planung und Entwicklung von Erdölraffinerien.

Im Jahre 1979 entwickelte der Russe Khasian einen neuen Algorithmus, mit dem bei linearen Optimierungsproblemen mit einer großen Anzahl von Variablen und einschränkenden Bedingungen die optimale Lösung schneller bestimmt werden konnte. Der wesentliche Vorteil dieses Verfahrens liegt darin, dass der Rechenaufwand geringer ist, als beim Simplexverfahren. Heute gehört die lineare Optimierung zu den best erforschten Gebieten der Wirtschaftsmathematik.

3. Graphisches Verfahren

3.1 Aufgabenstellung

Eine Unternehmung stellt zwei Produkte P und P her. Die Fertigung erfolgt auf den Maschinen M , M und M und erfordert unterschiedliche Belegungszeiten. Die Bearbeitungsdauer (bezogen auf Minuten) und die Kapazitäten (bezogen auf Mengeneinheiten) der Maschine sind in der folgenden Tabelle angegeben.

Der Deckungsbeitrag pro ME beträgt 90 GE von P und 120 GE von P

Wie viele ME sind von P und von P herzustellen, damit der gesamte Deckungsbeitrag möglichst groß ist. Wie hoch ist dieser maximale Deckungsbeitrag?

xi sei die Zahl der Produkte Pi

Z = 90x + 120x } Zielfunktion

20x + 40x Maschine M

15x + 10x Maschine M

30x + 10x 5400 Maschine M

x1 0

x2 Nichtnegativitätsbedingungen

Die Zielfunktion ist das Optimierungskriterium, welches minimal oder maximal werden soll.

In diesem Fall geht es um den Deckungsbeitrag, der maximal werden soll.

Die Nebenbedingungen sind Restriktionen (Beschränkungen), die sich in diesem Fall aus den Kapazitätsbeschränkungen der Maschinen ergeben.

Es gibt nämlich keinen Sinn negative Werte für x und x zuzulassen, denn die produzierte Menge kann nicht negativ sein. Deshalb unterliegen die Variablen x und x den Nichtnegativitätsbedingungen.

3.2 Graphische Lösung

Für Systeme mit zwei Variablen lassen sich die möglichen Lösungsmengen in einer Ebene (zweidimensional) graphisch veranschaulichen:

Für das Gleichheitszeichen wird mit jeder Nebenbedingung eine Gerade definiert, die die Ebene in zwei Halbebenen teilt.

Durch das Ungleichheitszeichen wird die Halbebene spezifiziert, in der die mögliche Lösungsmenge liegt. Im Ergebnis entsteht ein Polygon (=Vieleck).

Dazu stellt man zunächst die Nebenbedingungen nach x um.

20x + 40x / - 20x

40x 8000 - 20x / : 40

x 200 - 0,5x

x 300 - 1,5x

x 540 - 3x

Die Zielfunktion löst man auch nach x auf:

Z = 90x + 120x

3 Z

x

4 120

Die Graphen dieser Funktionenschar sind parallele Geraden, die danach unterschieden werden können, in welchen Punkten

PZ

„ Z †

¦0/ —————¦ sie die y- Achse schneiden.

… 120 ‡

Man konstruiert die Gerade der Zielfunktion für Z = 0.

Die Gerade wird solange parallel nach oben verschoben, bis sie an einem Eckpunkt das Polygon verlässt. Dieser Eckpunkt ist ein Optimum unseres Problems.

Z=0 : 3 0

x = - --- x

3

x = - --- x

PMAX ist der optimale Punkt. Man erzielt den höchsten Deckungsbeitrag, wenn 100 ME von P und 150 ME von P hergestellt werden.

Berechnung des maximalen Deckungsbeitrags:

ZMax = 90x + 120x

= 90*100 + 120*150

= 27000

Der maximale Deckungsbeitrag beträgt 27000 GE.

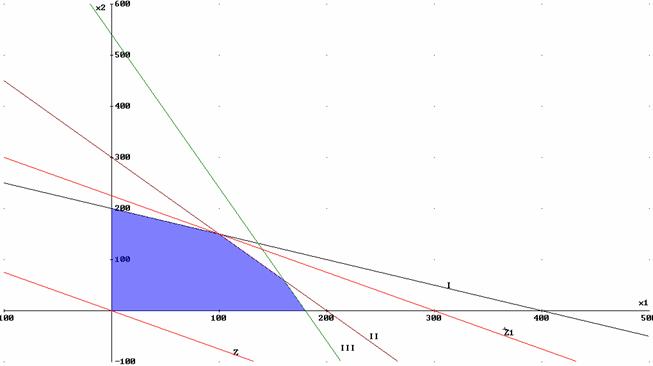
I    x 200 - 0,5x

II x 300 - 1,5x

III x 540 - 3x

Z = - 0,75x (Parallelverschiebung von Z nach Z

4. Die reguläre Simplexmethode

Das graphische Verfahren zur Lösung von linearen Optimierungsproblemen ist nur anwendbar bei zwei, höchstens drei Variablen. Aber schon bei drei Variablen trifft man auf erhebliche Schwierigkeiten, weil drei Variablen eine räumliche Darstellung in der Zeichenebene verlangen.

Bei n Variablen werden die Lösungsmengen von Hyperebenen im n - dimensionalen Raum begrenzt.

Es ensteht ein Polyeder (= Vielflächner).

Die Simplexmethode ist eine algebraische Methode, die es ermöglicht, lineare Optimierungsprobleme mit beliebig vielen Variablen einfach und übersichtlich zu lösen.

Ein Simplex ist ein Polyeder des R n (n - dimensionalen Raums) mit n + 1 Ecken.

zum Beispiel:                        R : Dreieck R : Tetraeder

Das Simplexverfahren ist ein Iterationsverfahren (schrittweises Rechenverfahren zur Annäherung an die exakte Lösung).

Man beginnt mit einer Startnäherung (meist xi = 0) und verbessert sukzessive (allmählich eintretend) die Zielfunktion.

Das Verfahren wird an dem obigen Beispiel erläutert:

a) Durch Einführen von Schlupfvariablen (ui 0) wird das Optimierungsproblem als lineares                                 

Gleichungssystem formuliert.

Die Schlupfvariable füllt den noch vorhandenen "Spielraum" aus, wenn die Werte für x

und x des linken Teils der Ungleichung kleiner als der Wert des rechten Teils sind.

Die Schlupfvariablen u , u und u übernehmen also die Werte der jeweils noch freien

Kapazität der Maschinen M , M und M

20x + 40x + u

15x + 10x + u

30x + 10x + u

90x + 120x = Z

(4 Gleichungen, 6 Unbekannte)

Basisvariable: Variable, die nach Vorgabe von zwei Variablen berechnet wird

(u , u , u

Nichtbasisvariable: frei vorgebbare Variablen (= 0)

(x , x

b) Startpunkt:    x1 = x2 = 0 (Nichtbasisvariablen)

Berechnen der Basisvariablen

I u = 8000 - 20x - 40x

II u = 3000 - 15x - 10x

III u = 5400 - 30x - 10x

IV Z = 90x + 120x

u

u

u

Z = 0

Bei dieser Ausgangslösung hat die Zielgröße den Wert Null; die Lösung ist im Sinne der Maximierung von Z aber eine "schlechte" Lösung.

c) Zur Verbesserung der Lösung soll nun ein Variablenaustausch erfolgen. Da x den größten

Einfluss auf die Zielfunktion hat, wird x in die Basis aufgenommen (x hat den größten

Einfluss auf die Zielfunktion, da der Deckungsbeitrag um 120 GE steigt, wenn der Wert

von x um eine ME steigt. Bei x steigt der Deckungsbeitrag nur um 90 GE).

Gegen welche Variable wird x getauscht?

x = 0, u

Versuch 1: x u :

aus I folgt:

x u = 8000 - 20x - 40x / - 8000 + 20x

u - 8000 + 20x = - 40x

- 8000 = - 40x / : (- 40)

x

aus II folgt:

u u = 3000 - 15x - 10x

u

u

aus III folgt:

u u = 5400 - 30x - 10x

u

u

	x = 0, u

Versuch 2: x u :

aus II folgt:

x u = 3000 - 15x - 10x / - 3000 + 15x

u - 3000 + 15x = - 10x

- 3000 = - 10x / : (- 10)

x

aus I folgt:

u u = 8000 - 20x - 40x

u

u ( Widerspruch, da u < 0 !)

ui

	x = 0, u

Versuch 3: : x u :

aus III folgt:

x u = 5400 - 30x - 10x / -5400 + 30x

u - 5400 + 30x = -10x

-5400 = -10x / : -10)

x

aus II folgt:

u u = 3000 - 15x - 10x

u

u ( Widerspruch, da u < 0 !)

i