Hyperreelle Zahlen

Hyperreelle Zahlen

Teil 1: Einführung in die Hyperreelen Zahlen und einige Eigenschaften

Zugang zu den hyperreellen Zahlen über das Berechnen der Steigung von Kurven

z.B.

durchschnittliche Steigung =

Da

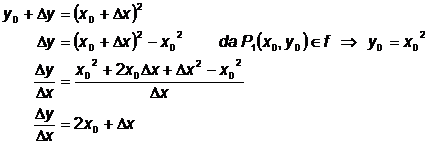
diese Operation nur erlaubt, wenn Dx

Je kleiner Dx wird, um so näher liegen die Punkte P₁ und P₂ beieinander die Steigung der Kurve in P₁ ist also nahe bei . Da Dx nahe bei 0 liegt, können wir es vernachlässigen und sagen:

Steigung = 2x₀

Die Entscheidung, ab wann eine reelle Zahl wie Dx klein genug ist, um vernachlässigt zu werden, ist definitionsbedürftig: die hyperreellen Zahlen R^* setzen sich aus den reellen Zahlen und den Infinitesimalen zusammen.

DEF.: Infinitesimale

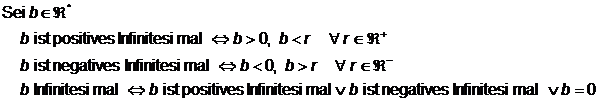
0 ist die einzige reelle Zahl, die auch Infinitesimal ist!

Für Hyperreelle Zahlen gelten alle bekannten Gesetze (bis auf das Archimedische Axiom) der reellen Zahlen (Abgeschlossen-heit bzgl. Addition, Multiplikation, Distributiv-, Assoziativ-, Kommutativgestze,.).

Bezeichnung für Infinitesimale: Dx Dy e d

Neben diesen sind aber noch andere Gesetze zu beachten:

1. Ist e ein positives Infinitesimal, so ist -e ein negatives Infinitesimal.
2. Ist e ein positives Infinitesimal und r eine reelle Zahl, so ist r+e eine hyperreelle Zahl.
3. Ist e ein positives Infinitesimal und a eine reelle Zahl, so ist ae ein positives Infinitesimal.
4. Ist e ein positives Infinitesima, so ist  ein positives und - ein negatives Infinitesimal.

DEF.: endlich, positiv unendlich, negativ unendlich

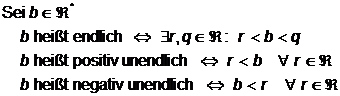
THEOREM 1: Regeln für Infinitesimale, Endliche und Unendliche Zahlen

Seien e d Infinitesimale, b,c hyperreelle Zahlen, die endlich aber keine Infinitesimale sind und H,K sind unendliche hyperreelle Zahlen.

(i)         Negative:

e ist infinitesimal

-b ist endlich, aber nicht infinitesimal

-H ist unendlich

(ii)       Kehrwerte:

 ist unendlich, e

 ist endlich, aber nicht infinitesimal

 ist infinitesimal

(iii)     Summen:

e d ist infinitesimal

b + e ist endlich, aber nicht infinitesimal

b + c ist endlich (evt. infinitesimal)

H + e und H + b sind unendlich

(iv)      Produkte:

d e und b e sind infinitesimal

b c ist endlich, aber nicht infinitesimal

H b und H K sind unendlich

(v)        Wurzeln:

ist infinitesimal, e > 0

endlich, aber n. infinitesimal, b > 0

 ist unendlich, H > 0

THEOREM 2:

(i)     Jede hyperreelle Zahl, die zwischen zwei Infinitesimalen liegt, ist infinitesimal.

(ii)           Jede hyperreelle Zahl, die zwischen zwei endlichen Zahlen leigt, ist endlich.

(iii)         Jede hyperreelle Zahl, die größer als irgendeine positiv unendlich Zahl ist, ist positiv unendlich.

(iv)         Jede hyperrelle Zahl, die kleiner als irgendeine negativ unedliche Zahl ist, ist negativ unendlich.

DEF.: unendlich nahe

Zwei hyperrelle Zahlen b und c nennt man unendlich nahe beieinander, , wenn ihre Differenz b - c infinitesimal ist.  bedeutet, dass b nicht undendlich nahe bei c liegt.

Anmerkungen:

Ist e infinitesimal, dann gilt: b b e Da Differenz b - (b - e e infinitesimal.

b ist infinitesimal b

b,c reell und b c T b = c

THEOREM 3:

Seien a, b, c hyperreelle Zahlen.

(i)      a a

(ii)            a b T b a

(iii)          a b, b c T a c

THEOREM 4:

Sei a b. Dann gilt:

(i)      a infinitesimal T b infinitesimal

(ii)            a endlich T b endlich

(iii)          a unendlich T b unendlich

DEF.: Standard Parts

Sei b eine endlich hyperreelle Zahl.

Unter dem Standard Parts von b, st(b), versteht man die reelle Zahl, die unendlich nahe bei b liegt. Unendlich hyperreelle Zahlen besitze keine Stadard parts.

THEOREM 5:

Seien a, b endlich hyperreelle Zahlen. Dann gilt:

(i)      st(-a) = - st(a)

(ii)            st(a+b) = st(a) + st(b)

(iii)          st(a-b) = st(a) - st(b)

(iv)          st(ab) = st(a) st(b)

(v)            Wenn st(b) 0, dann  st(a/b) = st(a)/ st(b)

(vi)          st(aⁿ) = (st(a))ⁿ

(vii)        Wenn a 0, dann

(viii)      Wenn a b, dann st(a) st(b)

Beweis:

(i)         st(-a) = - st(a)

Wir zeigen, dass -a unendlich nahe bei -r ist, mit -r = st(-a).