Die Transzendenz der Zahle

Die Transzendenz der Zahl e

Die Frage, ob eine Zahl transzendent (nicht algebraisch) oder algebraisch ist, kann man mit Hilfe der algebraischen Gleichung leicht beantworten.

Definition: Eine Zahl x heißt algebraisch, wenn sie folgende Gleichung erfüllt:

, wobei

"algebraische Gleichung"

Eine Zahl x heißt transzendent, wenn sie nicht algebraisch ist.

z.B. ist Lösung der Gleichung

Also sind rationale Zahlen algebraisch und daher nicht transzendent, da sie die allgemeine Gleichung

für erfüllen.

Aus diesem Grund können nur irrationale Zahlen transzendent sein, wobei sich die Frage stellt, ob wirklich alle irrationalen Zahlen oder nur bestimmte transzendent sind.

z.B. ist Lösung der Gleichung , woraus folgt, daß algebraisch ist, obwohl sie eine irrationale Zahl ist.

Aus diesem Beispiel können wir folgern, daß alle Wurzeln Lösungen von algebraischen Gleichungen (d.h. algebraisch) sind.

Wir können somit sehen, daß fast alle gebräuchlichen Zahlen algebraisch sind. Uns sind jedoch schon nach kurzem Überlegen zwei Ausnahmen bekannt: und e

Für e wollen wir nun den Beweis führen, wobei wir die Irrationalität von e voraussetzen.

Der erste Beweis der Transzendenz von e stammt von Hermite aus dem Jahre 1873. Der hier vorgestellte Beweis ist von David Hilbert 1893 und stellt eine Vereinfachung des Beweises von Hermite dar.

BEWEISIDEE

Die zentrale Idee des Beweises ist die Zerlegung der Zahl e in folgender Weise:

(R_n wird als Cauchy Rest bezeichnet)

Teil 1 läßt sich als Bruch darstellen:

mit

Daraus folgt: ist ganzzahlig.

Teil 2:

, so daß nicht ganzzahlig ist

Aus diesen beiden Teilen folgt, daß e durch rationale Zahlen besonders gut angenähert werden kann. Allgemein kann jede Zahl x durch rationale Zahlen beliebig nahe approximiert werden, wenn . Bei Zahlen, die schlecht durch rationale Zahlen angenähert werden können, kann es notwendig werden, den Nenner von r sehr groß zu wählen (so groß wie ).

Für e benötigen wir jedoch keinen so großen Nenner, da z.B. schon eine Approximation mit
n = 5 schon auf genau ist.

Der Beweis der Transzendenz von e hängt ab von der Erweiterung der Idee, e kann durch Brüche besonders gut approximiert werden, daß auch die endlichen Potenzen von e durch Brüche angenähert werden können.

Für den indirekten Beweis nehmen wir an, daß e algebraisch ist. Das heißt wir gehen davon aus, daß die algebraische Gleichung

für ganzzahlige Koeffizienten erfüllt wird.

Um einen Widerspruch zu erlangen, ist es notwendig bestimmte "Ganzzahlen" M, M₁,.,M_n und "Kleinzahlen" I I_n zu definieren, so daß

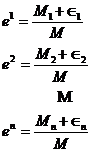
Nun stellt sich die Frage, wie klein die I's sein müssen. Dazu setzen wir die Ausdrücke in die algebraische Gleichung ein:

       multipliziert mit M

erhalten wir:     

Der erste Ausdruck ist eine ganze Zahl, und wir wählen die M's so, daß dieser Ausdruck notwendigerweise eine ganze Zahl ungleich 0 wird (Nichtnullganzzahl).

Man kann die I's auch so wählen, daß

Dies wird uns zum Widerspruch führen, da die Summe einer Nichtnullganzzahl und einer Zahl mit dem Absolutbetrag < nicht 0 sein kann.

Für den Beweis benötigen wir die G-Funktion.

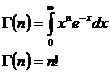
SATZ: e ist transzendent

BEWEIS:

Annahme: Es gibt Ganzzahlen a₀,..,a_n, wobei a₀ 0 ist, so daß

Man definiere Zahlen M, M₁,.,M_n und I I_n wie folgt

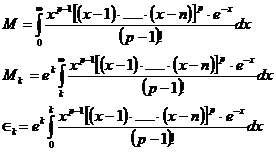
Das p stellt eine Primzahl dar, die später noch näher erklärt und bestimmt wird.

Zuerst betrachten wir M:

Wenn wir nun die Ausdrücke in den eckigen Klammern ausmultiplizieren, erhalten wir ein Polynom mit ganzzahligen Koeffizienten .

Gesteigert um die p-te Potenz entsteht folgendes Polynom:

Folglich kann M in der Form

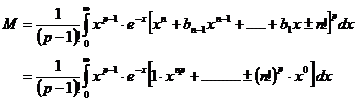
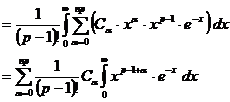
wobei C_a bestimmte Ganzzahlen sind und ist.

Von der G-Funktion wissen wir, daß

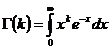durch partielles integrieren zu wird.

Daraus folgt daß

1) Für erhalten wir den Term

Wir betrachten nun Primzahlen p > n. Dann ist der Term eine ganze Zahl, welche nicht durch p teilbar ist. C₀ ist also nicht durch p teilbar.

2) Für gilt:

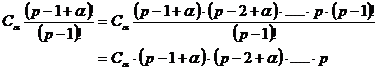
ist teilbar durch p für .

Aus 1 und 2 folgt, daß M eine Ganzzahl und nicht teilbar durch p ist.

Nun betrachten wir M_k:

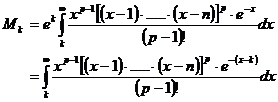
Durch Substitution x = k+u, du = dx erhalten wir den Ausdruck:

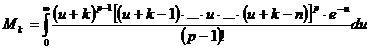
Die untere Grenze des Integrals wurde von k auf 0 geändert, da .

Der signifikante Unterschied zwischen M und M_k ist, daß im Ausdruck M_k der Faktor u an der k-ten Stelle vorkommt. Folglich beinhaltet die p-te Potenz den Faktor u^p. Das bedeutet, daß der gesamte Term

ein Polynom mit ganzzahligen Koeffizienten ist,

das zumindest Grad p besitzt

Es folgt:

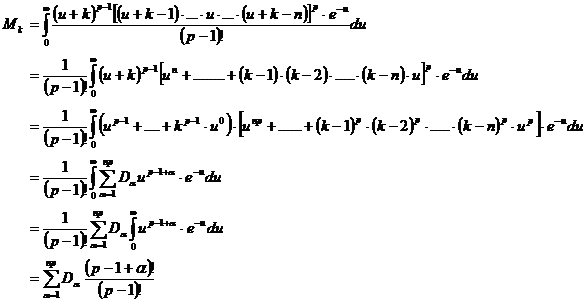
Da a mit 1 beginnt, ist der kleinstmögliche Term

Also ist D₁ durch p teilbar.

Dies gilt auch für a > 1, woraus folgt, daß alle Terme durch p teilbar sind. Somit sind alle M_k durch p teilbar.

Nun ist klar, daß

für k = 1,.,n

Eingesetzt in die algebraische Gleichung und multipliziert mit M, erhalten wir:

Zusätzlich zur Bedingung p > n vereinbaren wir, daß   (p kann somit nicht Teiler von a₀ sein. Das bedeutet, daß beide, M und a₀, nicht durch p teilbar sind, also auch nicht das Produkt der beiden.

Obwohl jedes M_k durch p teilbar ist (M aber nicht), folgt, daß nicht durch p teilbar ist. Dadurch ist der Ausdruck eine Nichtnullganzzahl.

Um einen Widerspruch zu erhalten und so zu beweisen, daß e transzendent ist, ist es nur mehr notwendig zu zeigen, daß so klein wie erforderlich gemacht werden kann, indem p groß genug gewählt wird.

Es reicht zu zeigen, daß jedes beliebig klein gemacht werden kann. Das erfordert einfache Abschätzungen. Für die weitere Beweisführung ist es wichtig sich zu erinnern, daß n eine feste Zahl (Grad der algebraischen Gleichung) ist.

Wenn , dann ist

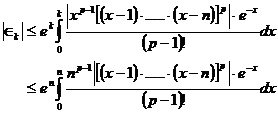
A sei das Maximum von für

Dann ist:

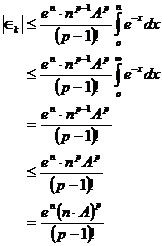
kann beliebig klein gemacht werden, indem man p beliebig groß wählt.