Mathematikformelsammlung 2

Totales Differential :                                                                       

Funktionsdifferenz : Du = u₁ -u₀ Bsp.: u = x + 2y² x₀ = 2 Dx = 0,2

y₀ = 1 Dy = 0,1

u₀ = 2 + 2 * 1² u₀ = 4 in die Fkt. die Werte x₀ und y₀ eingesetzt

u₁ = 2,2 + 2 * 1,1² u₁ = 4,62 in die Fkt. die Werte x₀ +Dx und y₀ +Dy eingesetzt

Du = u₁ -u₀ Du = 4,62 - 4 = 0,62

Fehlerrechnung :

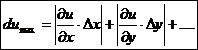
max. Fehler:    

mittlere Fehler :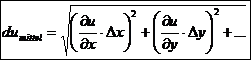

Extrema von Funktionen zweier Variablen:                   und und ..

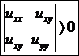
Für die Bestimmung Maxima/ Minima :

Determinante < 0 Sattelpunkt

Determinante = 0 Keine Entscheidung möglich

Determinante > 0 Maxima u_xx < 0 , u_yy < 0

Minima u_xx > 0 , u_yy > 0

Ausgleichsgerade:      2 Gleichungen mit

2 Unbekannten

"m" und "b" unbekannt

Komplexe Zahlen: z = a + bj

z = r e ^{j j} a = r cos j b = r sin j

Wichtig Quadrant beachten !!!

Potenzen mit komplexe Zahlen : Bsp.:

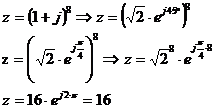
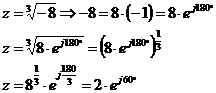Wurzeln mit komlexen Zahlen : Bsp.:

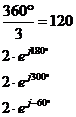
Weitere Lösungen :

Alle weiteren Lösungen sind um 120° verschoben

Logarithmus mit komplexen Zahlen :?

Mehrfachintegrale : u = f_(x,y)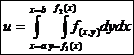

Erst die Fkt. nach y integrieren und die f_(x)-Grenzen einsetzen,

die neue Funktion nach x integrieren und die x-Grenzen einsetzen

Schwerpunkt von Flächen (Flächenschwerpunkt) , statisches Moment :

statisches Moment y - Achse :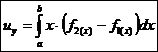      

statisches Moment x - Achse :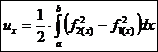      

Schwerpunkt :         

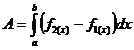
Schwerpunkt eines Drehkörpers um x - Achse :

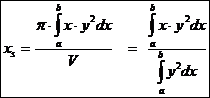
V = 2 A p y_s Volumen Drehkörpers :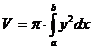

Trägheitsmomente ( 2. Flächenmoment ) :

Wichtig in dieses " y² " nicht die Funktion einsetzen , sondern nach y integrieren  !!!

Massenträgheitsmoment : 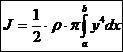f_(x) hoch 4 nehmen !!!

Mac'Laurin Reihe :

Vorraussetzung :

f_(x) ist für x=0 beliebig oft differenzierbar

die entstehende Reihe muß konvergent sein

Taylorreihe :

Differentialgleichungen :

a)     1. Ordnung mit TDV (Trennen der Variablen) y` = g_(x,y)

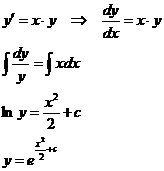
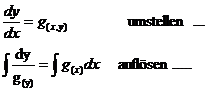
Bsp. :

Wichtig "c" nicht vergessen !!!

Dies ist die allgemeine Lösung !!!

Um "c" zu bekommen, ggf. die

Anfangsbedingung einsetzen und nach "c" auflösen

b) Variation der Konstanten :

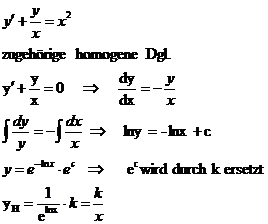
Bsp.:                                                                                                                      

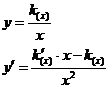Ansatz :

Diesen Ansatz in die Dgl. Einsetzten :

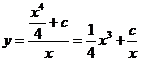
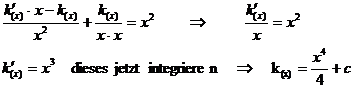
dieses entstandene k_(x) in die homogene Dgl. Einsetzen :                                                                                          

Lineare Dgl. 2. Ordnung mit konstanten Vorzahlen :

Lineare Dgl.: y , y´ , y´´ kommen nur in der ersten Potenz vor, auch nicht als Produkte.

Dagegen dürfen beliebige Ausdrücke mit "x" vorkommen.

a)     homogene Dgl. mit konstantan Vorzahlen : Lamda - Verfahren

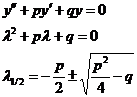Bsp.:

3 verschiedene Möglichkeiten bei der Lsg. der PQ-Formel :

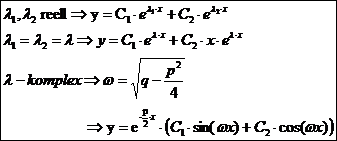
b) inhomogene Dgl. mit konstanten Vorzahlen :

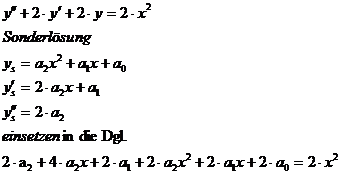
Bsp.:                                                                                                  

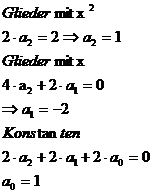
Konstanten in die y_s einsetzen :

zugehörige homogene Dgl. :

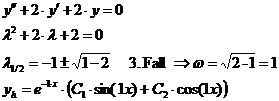
Gesamtlösung :

Nährungsverfahren :

a)     Streckenzugverfahren :

Bsp.:    

b)     Runge - Kutta - Verfahren :

                            

Massenträgheitsmomente :

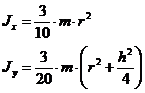Kugel : Zylinder voll : Stab lang , dünn :

Kegel :