Die Kurvendiskussion

Die Kurvendiskussion

Sinn und Zweck einer Kurvendiskussion

Eine Kurvendiskussion versucht etwas über die Eigenschaften einer Funktion herauszufinden, ohne dass man die Funktion dafür zeichnen muss. Die Kurvendiskussion liefert einem Aussagen über das Verhalten der Funktion, so dass man den Graphen danach besser zeichnen kann. Wenn man eine Wertetabelle erstellt, bekommt man eine bestimmte Anzahl von Punkten des Funktionsgraphen. Mit diesen verbindet man die Hoffnung, dass die Funktion auch so verläuft. Hat man aber zum Beispiel eine Definitionslücke übersehen, zeichnet man etwas Falsches. Die Kurvendiskussion löst dieses Problem, denn richtig durchgeführt gibt sie einem alle Informationen die man haben muss.

1. Definitionsmenge

Zuerst muss man die Definitionsmenge bestimmen. Bei ganzrationalen Funktionen ist dies einfach, bei gebrochen rationalen Zahlen ist auf die Nullstellen des Nenners zu achten.

2. Symmetrie zum Koordinatensystem

Die Symmetrie zum Koordinatensystem ist wie folgt zu untersuchen:

• Ist f(-x) =  f(x) so ist der Graph der Funktion achsensymmetrisch zur y-Achse.
• Ist f(x) =  - f(-x) so ist der Graph der Funktion punktsymmetrisch zum Ursprung also (0|0).

3. Nullstellen

Die Nullstellen einer Funktion f sind ganz allgemein durch die Lösungen der Gleichung

f(x) = 0

gegeben. Sie entsprechen jenen Punkten, an denen der Graph die x-Achse schneidet.

4. Steigung des Funktionsgraphen

Mit Hilfe der Ableitungsfunktion f' kann man die Steigung des Graphen von f untersuchen. Dazu sei im Folgenden f als stetig d.h. ihr Graph ist eine zusammenhängende Linie) differenzierbar vorausgesetzt.

Ist f'(x₀)>0, dann ist f in einer Umgebung der Stelle x₀ streng monoton steigend.

Ist f'(x₀ <0, dann ist f in einer Umgebung der Stelle x₀ streng monoton fallend.

Ist f'(x₀)=0, dann hat f an der Stelle x₀ eine zur x-Achse parallele Tangente ("waagrechte Tangente).

Ist f'(x₀)=0, dann kann f in einer Umgebung von x₀ durchaus monoton steigend oder monoton fallend sein, es ist aber auch möglich, dass die Steigung ihr Vorzeichen ändert.

6. Extrema (Hochpunkte und Tiefpunkte)

Unter den Extremwerten oder Extrema versteht man den höchsten bzw. niedrigsten Punkt eines Funktionsgraphen. Relative Extrema sind Extrema in einer bestimmten Umgebung. Die relativen Extremwerte im Inneren des Definitionsbereichs einer differenzierbaren Funktion f gehören zu Punkten mit waagrechten Tangenten. Die Bedingung f'(x₀) = 0 ist also notwendig dafür, dass x₀ ein Extrempunkt ist. Diese Bedingung ist aber nicht hinreichend, d.h. es gibt Punkte mit waagrechter Tangente, welche nicht Extrempunkte sind. Ein Extrempunkt liegt vor, wenn f' an der Stelle x₀ das Vorzeichen wechselt. Es sei im folgendem f zweimal stetig differenzierbar.

Ist f'(x₀) = 0 und f''(x₀) < 0, dann ist f' an der Stelle x₀ streng monoton fallend, es liegt also eine Maximalstelle vor.

Ist f'(x₀) = 0 und f''(x₀) > 0, dann ist f' an der Stelle x₀ streng monoton steigend, es liegt also ein Minimalstelle vor.

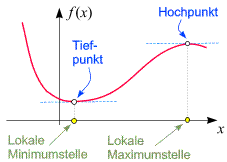
Für f'(x₀)=f''(x₀)=0 kann ein Extremum oder ein Wendepunkt mit waagrechter Tangente vorliegen, solch einen Wendepunkt nenn man Sattelpunkt.

Beispiel:

y= x³ - 15x² + 48x -3

y'= 3x² - 30x + 48

y''= 6x - 30

y' null setzen: 3x² - 30x + 48 = 0 L=

y''(x_E1) = 6*8 - 30 > 0 → Minimum E1= [8; -67]

y''(x_E2)= 6*2 - 30 < 0 → Maximum E2=[2; 41]

7. Krümmung des Funktionsgraphen

Ist f''(x₀)>0, dann ist f in einer Umgebung von x₀ linksgekrümmt oder eine Linkskurve.

Ist f''(x₀)<0, dann ist f in einer Umgebung von x₀ rechtsgekrümmt oder eine Rechtskurve.

Ist f''(x₀)=0, dann kann ein Wendepunkt vorliegen, es kann aber die Kurve auch ihren Krümmungssinn behalten.

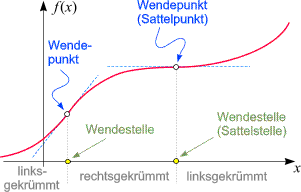
8. Wendepunkt des Funktionsgraphen

In einem Wendepunkt geht eine Linkskurve in eine Rechtskurve über oder umgekehrt, die zweite Ableitungsfunktion f''(x₀) ändert also ihr Vorzeichen.

Wendestellen einer Funktion f sind die Lösungen der Gleichung

f ''(x) = 0

Man setzt wieder voraus, dass die Lösung "isoliert" ist, d.h. dass es für jede Lösung ein Intervall (x-a, x+a) gibt (eine Umgebung von x), in dem die zweite Ableitung nur an der Stelle x verschwindet ansonsten überall ≠ 0 ist. Von jeder Lösung ist dann eigens zu überprüfen, ob es sich tatsächlich um einen Wendepunkt handelt.

Das in der Praxis einfachste Verfahren besteht darin, einige Werte von f' konkret auszurechnen und miteinander zu vergleichen, um festzustellen, ob die Stelle x ein lokales Extremum von f' ist.

Ist f''(x)=0 und f'''(x) ≠ 0, so ist x ein Wendepunkt von f. Ist f'''(x)=0, so lässt sich daraus keine Aussage machen, ob es sich um einen Wendepunkt handelt.

9. Unstetigkeiten einer Funktion

Pol x_p der Funktion f ist der Wert aus dem Definitionsbereich, bei dem der Funktionswert f(x_p) gegen ±∞ strebt (Unendlichkeitsstelle).

Bei rationalen Funktionen f(x_p) = gilt:

Lücken bei gebrochen rationalen Funktionen treten an den Stellen auf, wo Zähler und Nenner gleichzeitig verschwinden z.B.

y= an der Stelle x = 1, f(1) = .

10. Verhalten im Unendlichen, Grenzwert des Funktionswertes für x → ±∞

Für unbeschränkt wachsende (abnehmende) Argumente hat f den Grenzwert , Bedingungen siehe Grenzwert.

Ganzrationale Funktionen streben immer gegen +∞ oder -∞. Ausschlaggebend für das Verhalten im Unendlichen ist ausschließlich Vorzeichen und Grad des höchstgradigen Glieds des Polynoms.

f(x)= 2x² - 63000x + 8

Das Glied -63000x wird gegenüber 2x² sehr schnell unbedeutend, wenn x gegen ± ∞ geht. Die Funktion strebt also wie 2x² für x→+∞ gegen +∞ und für x→- ebenfalls gegen +∞.

Beispiel:

2x² - 63000 + 8= +∞

2x² - 63000 + 8= +∞

Gebrochenrationale Funktionen hingegen können auch ganz anderes Verhalten im Unendlichen zeigen. Tatsächlich kann eine gebrochenrationale Funktion, abhängig von den Graden des Zähler- und Nennerpolynoms, ganz verschiedene Verhalten im Unendlichen zeigen.

Ist der Zählergrad größer als der Nennergrad, divergiert die Funktion d.h. der Graph läuft gegen + oder - Unendlich.

Sind Zähler- und Nennergrad gleich, gibt es eine waagrechte Grenzkurve (= Asymptote) parallel zur x-Achse, an die sich der Graph annähert.

Ist der Zählergrad kleiner als der Nennergrad, nähert sich der Graph der x-Achse.

Beispiel:

= 2

= 2

Das Ergebnis zeigt, dass es eine waagrechte Asymptote gibt, die bei 2 durch die y-Achse läuft. Zähler und Nennergrad sind gleich.    

Asymptoten und Grenzkurven

Wie kann man feststellen, ob eine gegebene rationale Funktion Asymptoten besitzt und wie sie liegen?

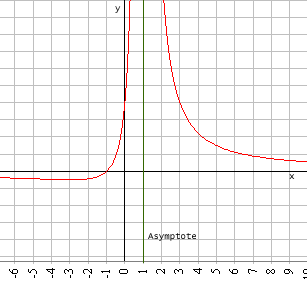
Wir betrachten die Funktion

f(x)=

Sie besitzt einen Pol, und zwar bei x = 1. Daher ist die 'vertikale' (zur y-Achse parallele) Gerade, auf der x = 1 gilt, eine Asymptote.

Um herauszufinden, wie sich die Funktion für |x| → ∞ verhält, benutzen wir die Tatsache, dass eine Potenz umso schneller wächst, je größer ihr Exponent ist. Wird x immer größer, so wächst x³ wesentlich schneller als x², und dieses wiederum schneller als x. Für große x kommt der Wert eines Polynoms in erster Linie durch seine höchste Potenz zustande.

Wir erhalten also einen ersten Eindruck vom 'asymptotischen Verhalten' unserer Funktion, wenn wir zuerst alle Klammern ausmultiplizieren.

f(x)=

und dann für Zähler und Nenner nur die höchsten Potenzen anschreiben:

f(x)≈ wenn |x| groß ist

Für |x| → ∞ verhält sich die Funktion also wie 1/x. Ihr Graph nähert sich der x-Achse. Daher ist die x-Achse eine Asymptote von f.

Wir betrachten die Funktion

f(x)=

Diesmal gibt es keinen Pol (da der Nenner immer ungleich Null ist), daher auch keine zur y-Achse parallele Asymptote. Es bleibt also, das Verhalten für |x| → ∞ zu untersuchen. Indem wir wieder nur die jeweils höchsten Potenzen in Zähler und Nenner berücksichtigen.

f(x)≈ wenn |x| groß ist

Für |x| → ∞ verhält sich die Funktion daher wie x², wächst also näherungsweise quadratisch. Ihr Graph nähert sich in dieser Näherung wie eine Parabel (und nicht wie eine Gerade). Daher hat die Funktion f überhaupt keine Asymptote.

Als nächstes betrachten wir die Funktion

f(x)=

Ihr Nenner kann als (x + 1) (x - 1) geschrieben werden, weshalb es nun zwei Pole (bei x = -1 und bei x = 1) gibt. Daher liegen zwei zur y-Achse parallele Asymptoten (bei x = -1 und bei x = 1) vor.

Das Verhalten im Unendlichen erschließt sich wieder durch unsere Methode, alle Klammern auszumultiplizieren und nur die höchsten Potenzen zu berücksichtigen:

f(x)≈ wenn |x| groß ist

Wir sehen, dass die Funktion für |x| → ∞ der Konstanten 2 zustrebt. Das bedeutet, dass der Graph der konstanten Funktion g(x) = 2 (d.h. die durch die Gleichung y = 2 beschriebene, zur x-Achse parallele Gerade) eine Asymptote ist.

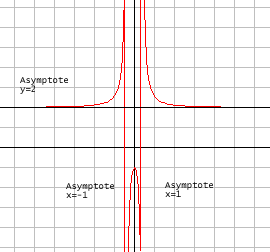
Allgemeine Aussagen über das Auftreten von Asymptoten

Zunächst halten wir fest, dass jeder Pol einer rationalen Funktion Anlass zu einer (zur y-Achse parallelen) Asymptote gibt.

Wie können wir ohne großen Aufwand erkennen, ob noch weitere Asymptoten existieren? Überlegen Sie, worin sich die obigen Beispiele voneinander unterscheiden! Vielleicht haben Sie es selbst erraten: Es sind die Ordnungen der Polynome in Zähler und Nenner, die für das Verhalten im Unendlichen relevant sind. Sehen wir uns das ein bisschen genauer an.

Eine rationale Funktion, also der Quotient zweier Polynome, ist immer von der Form

f(x)=

wobei der Zähler p ein Polynom n-ter Ordnung, der Nenner q ein Polynom m-ter Ordnung ist. Folgende Fälle können eintreten:

• Ist n < m, so strebt die Funktion für |x| → ∞ gegen Null. Daher ist die x-Achse eine Asymptote.

• Ist n = m, so strebt die Funktion für |x| → ∞ gegen eine Konstante. Daher existiert eine zur x-Achse parallele Asymptote, deren Lage sich unmittelbar aus dem Wert dieser Konstanten ergibt.
   

• Ist n > m + 1 (d.h. die Ordnung des Zählers zumindest um 2 höher als jene des Nenners), so nähert sich das Verhalten für große |x| einer Potenzfunktion mit Exponenten größer als 1. Daher existiert keine weitere Asymptote mehr.

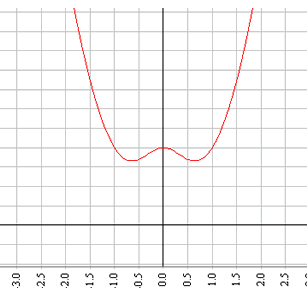
Diskussion der Gauss'schen Glockenkurve

Diskutiere die Funktion g(x)= 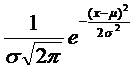   (σ > 0)

Lösung:

1. Größtmöglicher Definitionsbereich, Stetigkeit, Polstellen: Die Funktion ist für alle xR definiert; keine Unstetigkeiten und keine Polstellen (Unendlichkeitsstellen).
2. Symterie? Für = 0 ist die Funktion gerade, da in diesem Fall g(-x)=g(x). Für ≠ 0 ist die Funktion weder gerade noch ungerade.
3. Nullstellen

Da stets g(x) > 0, gibt es keine Nullstellen.

4. Verhalten im Unendlichen, Asymptoten

Wächst x über alle Schranken, so geht g(x) unbegrenzt nach 0: g(x)=0.

Das gleiche gilt, wenn x nach -∞ geht: g(x)=0. Die Gerade y=0, also die x-Achse, ist Asymptote der Funktion.

5. Extrema und Wendestellen

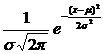g'(x)= *(2(x-μ))= -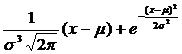

g''(x)= -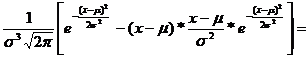

Mögliche Extremalstellen: g'(x)= -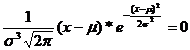

Die erste Ableitung ist nur null, wenn x = μ ist, da eine Exponentialfunktion stets positiv ist und daher nie null sein kann.

Da g''(μ)=-, ist x = μ eine Maximumstelle.

Wegen g(0)= = gilt für den Hochpunkt H(μ, ).

Mögliche Wendestellen: g''(x)= -**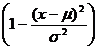= 0

Diese Gleichung ist nur null, wenn 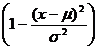= 0 ist. Daraus folgt (x-μ)²= σ²

oder weiter x - μ = ±σ oder x = μ ± σ.

Statt die 3. Ableitung zu berechnen und damit x = μ ± σ als Wendestellen zu bestätigen kann man wie folgt argumentieren: g''(x) wechselt an x = μ−σ sein Vorzeichen von + auf −, d.h. die Kurve wechselt an dieser Stelle von einer Links- zu einer Rechtskurve das bedeutet aber gerade, dass die Kurve an dieser Stelle einen Wendepunkt besitzt. Entsprechend folgert man an der Stelle x = μ+σ, wo das Vorzeichen von g''(x) von − auf + wechselt, dass die Kurve von einer Rechts zu einer Linkskurve übergeht.

Wegen   g(μ−σ)= 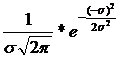= *= ist W_1.

Da g(μ + σ) = g(μ - σ) lautet der zweite Wendepunkt: W₂.

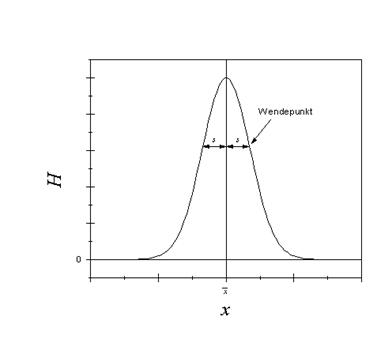
Jede Gauß'sche Glockenkurve besitzt also ein Maximum an der Stelle μ und zwei symmetrisch dazu liegende Wendepunkte an den Stellen μ − σ und μ + σ. Diese geben dem Graphen eine glockenförmige Gestallt.

g(x) ist die so genannte Dichtefunktion der Normalverteilung, die von fundamentaler Bedeutung in der Statistik ist. μ heißt Erwartungswert oder Mittelwert, σ Standardabweichung der Normalverteilung.

6. Graphen zeichen: Die Abbildung zeigt die Gauß'sche Glockenkurve.